DISTRIBUCIÓN BINOMIAL Y DISTRIBUCIÓN HIPERGEOMÉTRICA
Ruffiar Nicolás Maritza Paola 604
DISTRIBUCIÓN BINOMIAL
tiene las siguientes características:
- sólo son posibles dos resultados: el suceso (éxito) y su contrario (fracaso).
- El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
- La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de `A es 1- p y la representamos por q .
- El experimento consta de un número n de pruebas.
A la variable X que expresa el número de éxitos obtenidos en cada prueba del experimento, la llamaremos variable aleatoria binomial.
La distribución Binomial se suele representar por B(n,p) siendo n y p los parámetros de dicha distribución.
tiene 3 parámetros

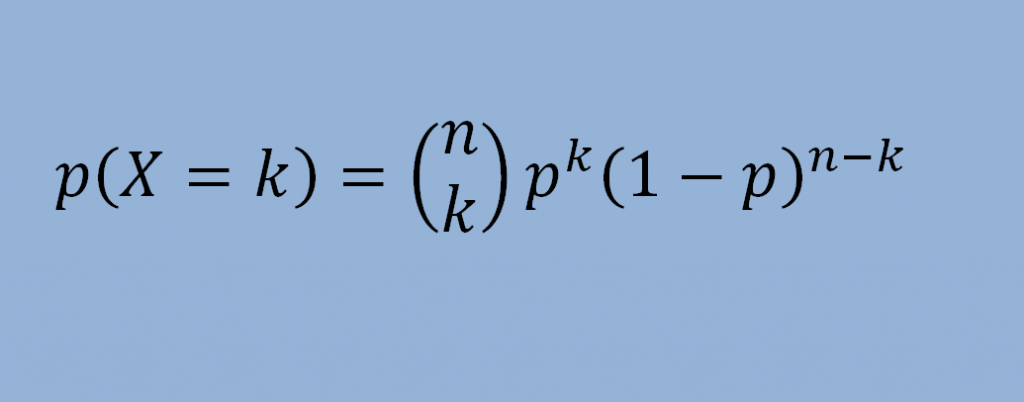
Ejemplo
Una máquina fabrica una determinada pieza y se sabe que produce un 7 por 1000 de piezas defectuosas. Hallar la probabilidad de que al examinar 50 piezas sólo haya una defectuosa.
Solución :
Se trata de una distribución binomial de parámetros B(50, 0'007) y debemos calcular la probabilidad p(X=1).

DISTRIBUCIÓN HIPERGEOMÉTRICA
se usa en los casos donde se extraen muestras o se realizan experiencias repetidas sin devolución del elemento que se extrajo o sin retornar a la situación experimental inicial. es fundamental en el estudio de muestras pequeñas y en el cálculo de probabilidades de juegos de azar. Sus aplicaciones se dan en el control de calidad para procesos experimentales en los que no es posible retornar a la situación de partida.
Las consideraciones a tener en cuenta son:
El proceso consta de "n" pruebas, separables de un conjunto de N pruebas posibles.
Cada una de las pruebas puede dar solo dos resultados mutuamente excluyentes
El número de individuos que presentan la característica A es "k"
En la primera prueba laS probabilidades son PA) = p y P(A)=q; con p+q= 1
En estas condiciones, se define la variable aleatoria X= n° de éxitos obtenidos
La función de probabilidad de esta variable sería
Las consideraciones a tener en cuenta son:
El proceso consta de "n" pruebas, separables de un conjunto de N pruebas posibles.
Cada una de las pruebas puede dar solo dos resultados mutuamente excluyentes
El número de individuos que presentan la característica A es "k"
En la primera prueba laS probabilidades son PA) = p y P(A)=q; con p+q= 1
En estas condiciones, se define la variable aleatoria X= n° de éxitos obtenidos
La función de probabilidad de esta variable sería




Comentarios
Publicar un comentario